[알고리즘 정리] DAG에서 최단경로를 찾는 법

DAG는 Directed Acyclic Graph 이다. 풀어서 써보면, 방향이 존재하고 사이클이 없는 그래프 라고 할 수 있다. 벨만-포트 알고리즘의 가장 큰 문제는 음수 사이클이 있는지 확인하기 위해 걸리는 시간이었다. 그러나 DAG에서는 사이클이 존재하지 않고, 방향이 있기 때문에 추가적인 연산없이 최단거리를 찾는 것이 가능할 것이다.

Algorithm Strategy

방향이 있고 사이클이 없는 그래프라는 것은 곧 모든 정점이 탐색되는 순서를 가진다는 것이다. 이 성질을 이용해서 한 정점으로부터 다른 정점으로 이동할 때의 최단거리를 추적해가다보면, 가장 마지막 정점에 도착하기까지 최단거리를 구할 수 있을 것이다. 이를 구현하기 위해서 다음과 같은 과정을 거친다.

1. Topological Sort 를 통해서 방문순서대로 정점을 정렬한다. 위상정렬이라고 부르는 Topological Sort는 여기에 정리해두었다.
2. 각 정점마다 Relaxation 을 진행해서 해당 정점과 연결되어 있는 정점들 중 최단거리를 찾는다.

Example

위와 같은 DAG가 있을 때, 최단 경로를 한번 찾아보자. 설명을 간소화하기 위해 이미 위상 정렬이 끝난 그래프를 사용했다.

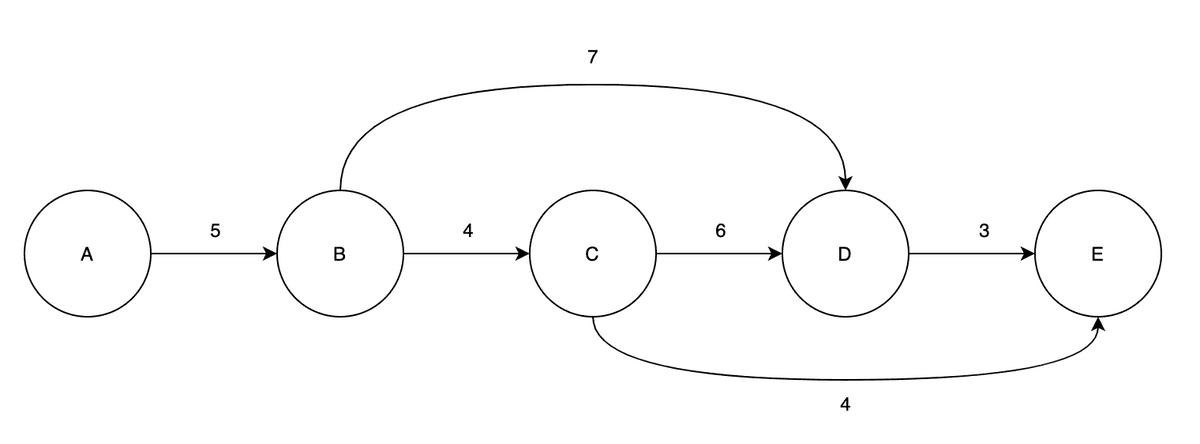
Phase 1

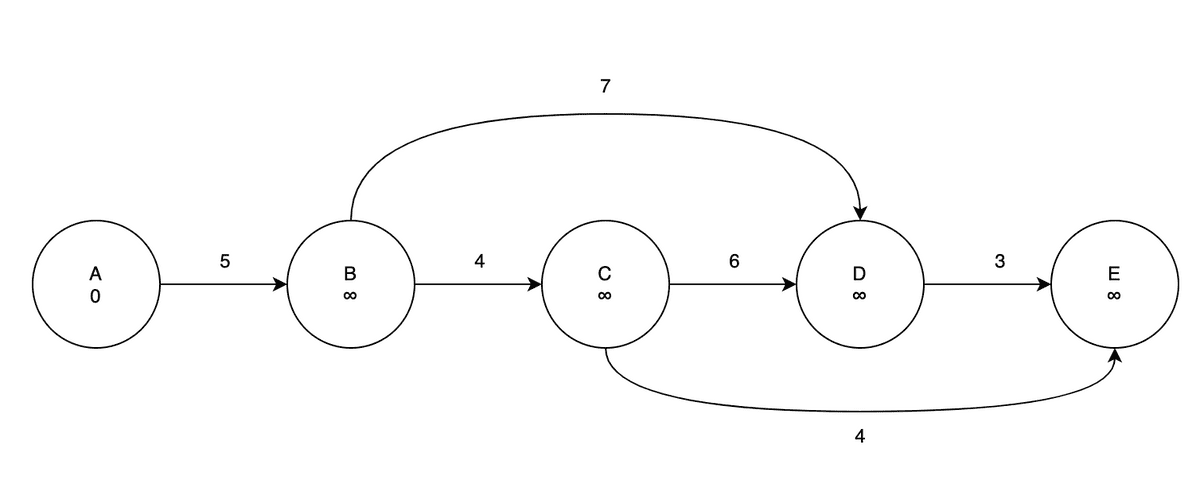
벨만-포드 알고리즘에서 했던 것처럼 모든 정점의 최단거리를 양의 무한대로 초기화 하고, 시작점이 되는 가장 앞에 있는 노드는 0으로 초기화 한다.

Phase 2

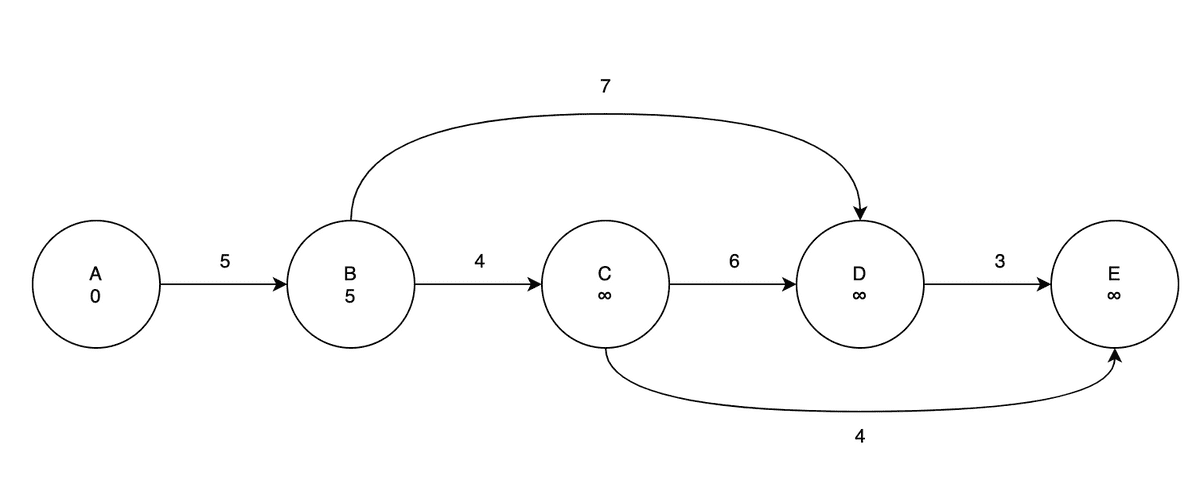
정렬된 정점들을 순서대로 꺼내서 Relaxation을 진행해보자. 일단 시작점에 있는 A에 대해서 Relaxation 을 수행하면, 연결된 정점이 B 하나뿐이기 때문의 B가 가지고 있는 최단거리와 A와 B 사이의 간선 거리를 비교해서 더 작은 값을 최단거리로 업데이트 한다. A와 B의 간선거리는 5이고, B의 최단거리는 양의 무한대로 초기화되어 있는 상태이기 때문에 B의 최단거리를 5로 갱신한다.

Phase 3

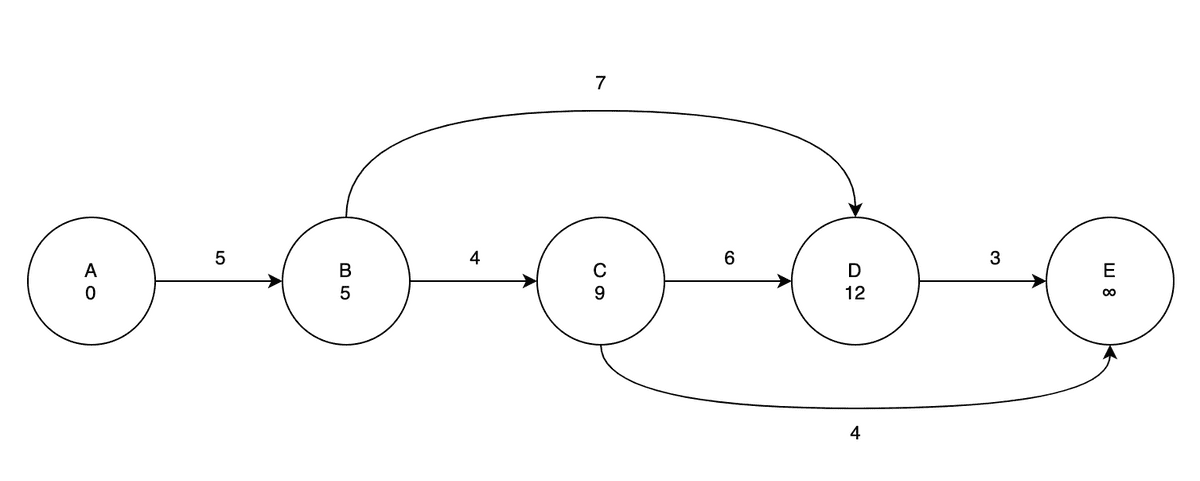
다음의 정점 B와 연결된 정점들의 대해서 Relaxation을 진행한다.

1. 정점 D: B까지의 최단거리는 5이기 때문에 정점 D까지 가는 간선 거리 7을 더하면 총 12의 거리를 얻는다. 현재까지 정점 D에 저장된 최단거리는 양의 무한대이므로, 새로운 최단거리 12을 설정한다.
2. 정점 C: 위와 같은 과정을 거쳐서 C의 최단거리를 5 + 4 = 9 로 갱신된다.

Phase 4

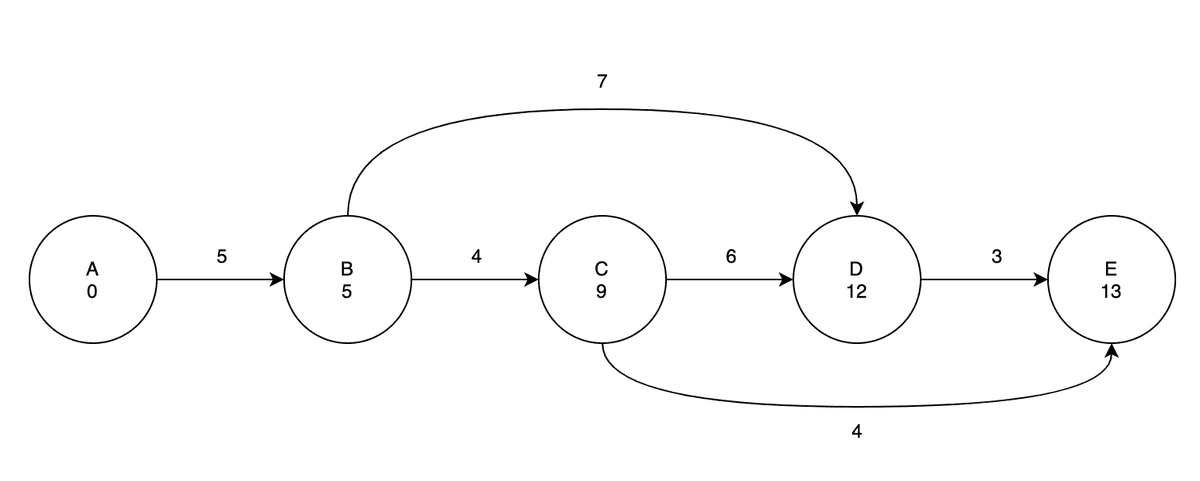
다음은 정점 C를 꺼내서 Relaxation을 해보자.

1. 정점 D: 정점 C가 가진 최단거리는 9이기 때문에, 정점 C에서 정점 D로 이동할 때 계산되는 최단거리는 9 + 6 = 15 이다. 현재 D에 저장된 최단거리는 12이기 때문에 정점 C를 거쳐서 D로 가는 경로는 최단경로가 아니다. 따라서 최단거리를 업데이트하지 않고 끝낸다.
2. 정점 E: 정점 E의 최단거리는 양의 무한대이기 때문에 C를 통해서 도달하는 경로가 최단거리로 업데이트될 것이다. E의 최단거리는 9 + 4 = 13이 된다.

Phase 5

D 노드에 대해서 Relaxation을 수행하게되면 E로 연결된 경로만 확인해주면 된다. D를 거쳐서 E로 가게되면 15의 거리가 발생한다. 현재 E로 가는 최단거리는 13이기 때문에 업데이트 하지 않는다.

Phase 6

마지막에 위치한 정점은 더 이상 연결할 정점이 없기 때문에 Relaxation을 수행하지 않고 마친다.

Algorithm Analysis

DAG에서 최단 경로를 구하는 시간복잡도는 다음과 같다.

1. 위상정렬을 수행하는 시간 𝛩(V+E)
2. 최초에 모든 정점을 초기화하는 시간 𝛩(|V|)
3. 각 정점에 대한 Relaxation을 수행하는 시간 𝛩(|E|)

따라서 최종 시간 복잡도는 위의 세 연산을 다 합쳤을 때의 점근표기인 𝛩(V+E) 가 된다.