[알고리즘 정리] 기수정렬(Radix Sort)

기수 정렬, Radix Sort

기수 정렬은 계수 정렬(Counting Sort) 와 마찬가지로 비교연산을 수행하지 않아 조건이 맞는 상황에서 빠른 정렬 속도를 보장하는 알고리즘이다. 전체적인 컨셉은 데이터의 각 자릿수를 낮은 자리수에서부터 가장 큰 자리수까지 올라가면서 정렬을 수행하는 것이다. 그리고 이런 이유 때문에 자릿수가 존재하지 않는 데이터를 기수정렬로 정렬하는 것은 불가능하다.

Algorithm Concept

기수 정렬은 다음과 같은 과정을 거쳐서 정렬을 수행한다. 예를 들어, 현재 가지고 있는 데이터 중 가장 큰 자릿수가 100의 자리라고 해보자.

1. 각 데이터들의 1의 자리를 비교해서 같은 데이터끼리 모은다. 1의 자리가 작은 데이터들이 앞에 위치하게 되고 큰 숫자들이 뒤에 위치하게 된다.(오름차순 기준)
2. 이때 같은 자릿수에 여러 데이터가 있을 경우에는 입력된 순서(나열된 순서)로 데이터를 모은다.
3. 2번까지 과정을 마치면 1의 자리가 가장 작은 숫자부터 가장 큰 숫자 순으로 데이터들이 정렬된다.
4. 이번에는 10의 자리가 같은 데이터끼리 오름차순으로 나열한다.
5. 10보다 작은 숫자들은 배열에 위치했던 순서대로 새로운 정렬의 제일 앞에 위치하게 된다.
6. 1이번에는 100의 자리가 같은 데이터끼리 오름차순으로 나열한다.
7. 100보다 작은 숫자들은 배열의 제일 앞에서부터 순서대로 채운다.
8. 데이터들의 최대 자릿수가 100의 자리이기 때문에 더 이상 진행하지 않고 종료한다.

이왜되? Let’s dive into example!

이게 왜 되지? 예시를 보면 이게 왜 되는지 직관적으로 와닿는다. 예시를 풀어보자.

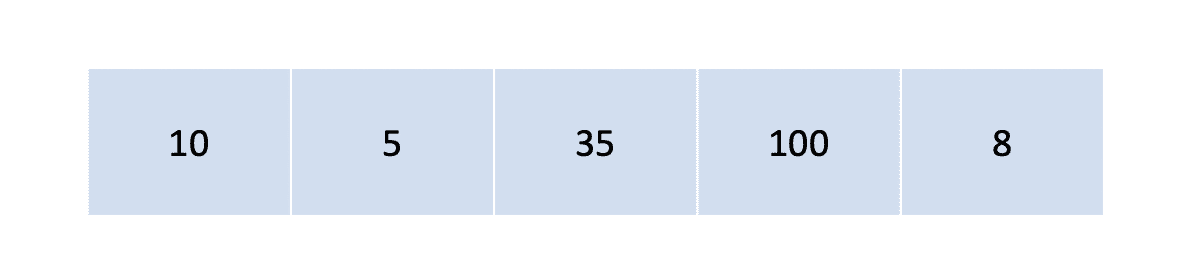
Phase 1

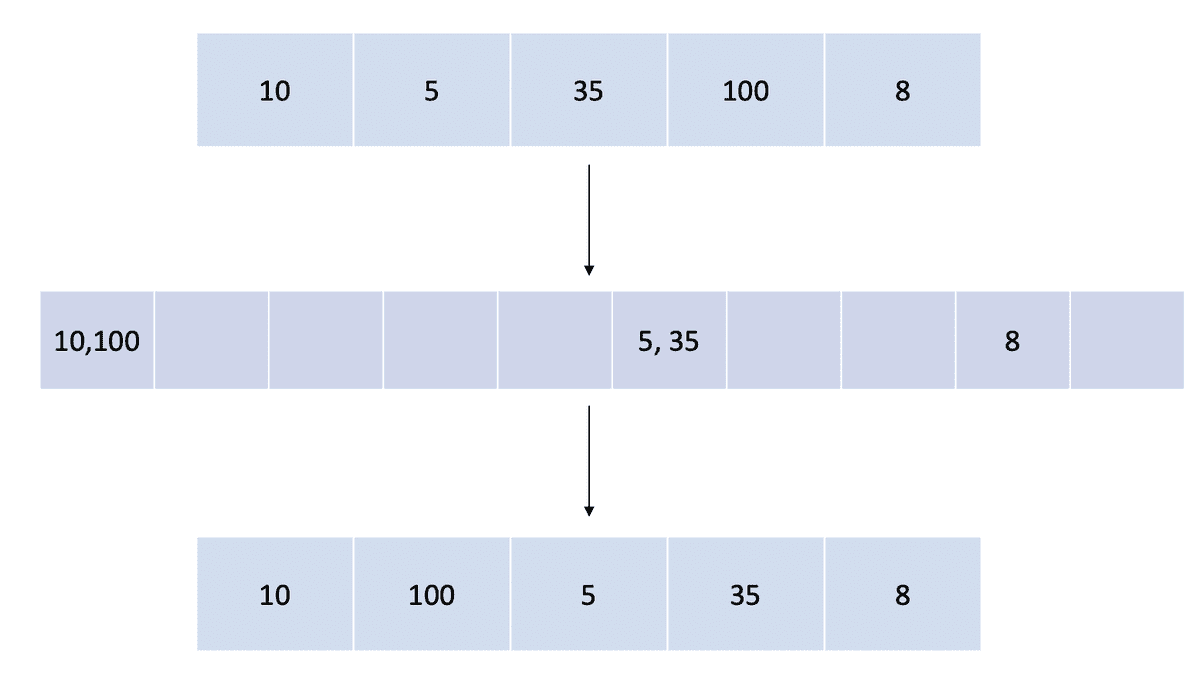
Phase 2

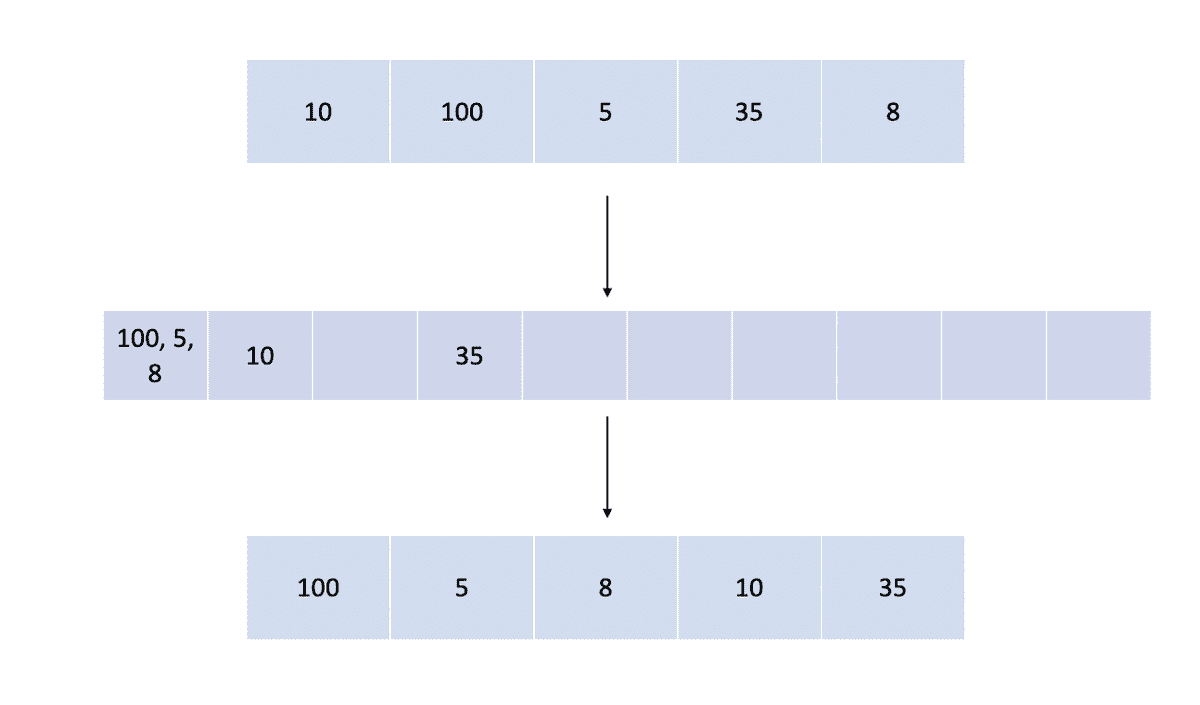
Phase 3

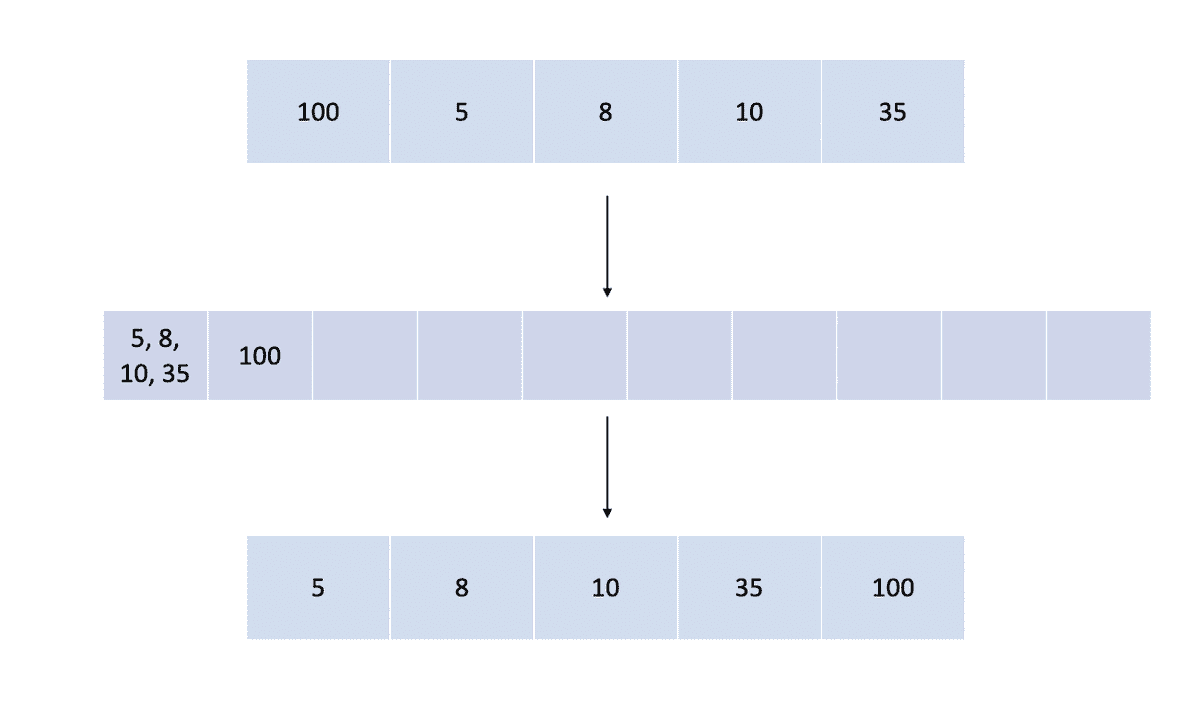
Algorithm Analysis

기수 정렬의 알고리즘은 Օ(dN) 이다. N은 데이터의 개수를 의미하고 d는 데이터들의 최대 자리수이다. 기수 정렬은 비교연산을 수행하지 않고 버킷에 데이터를 넣고 빼는 작업(N)을 최대 자릿수(d)만큼 만큼 반복하기 때문에 위와 같은 시간복잡도를 가지게된다.

그리고 기수정렬은 안정정렬 이다. 정렬 이후에도 중복된 값들은 자리가 뒤바뀌지 않는다.

마지막으로 기수정렬은 버킷이라는 추가적인 메모리 공간을 요구하게 된다. 그런데 더 큰 문제는 버킷의 크기를 모든 케이스에 맞게 딱 정의하기 어렵다는 것이다. 10 진수인 데이터들을 정렬하기 위해서는 0~9 를 저장할 10개의 공간이 필요하지만, 만약 알파벳을 정렬한다면 총 길이가 26인 버킷이 필요하다.